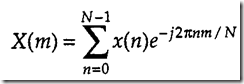sábado, 26 de enero de 2013
Detector de pulsos cardiacos fácil de hacer
Hola. Después de mucho tiempo voy a actualizar este blog. Esta vez les traigo un circuito para un PPG (Fotopletismógrafo, por su siglas en inglés). Se trata de un dispositivo capaz de detectar los latidos de corazón basándose en el echo de que un incremento en el flujo sanguíneo dejará pasar menos luz a través del dedo. Sabemos que con cada latido la sangre es bombeada por el cuerpo así que, es posible detectar estos latidos por medio de los cambios de permeabilidad luminosa a través del dedo.
El circuito empleado es muy simple:
En la parte inferior izquierda tenemos un circuito seguidor de tensión cuya única función es crear una fuente simétrica de ±2.5 V. Esto lo hice para poder alimentar a los amplificadores con una fuente simétrica y referenciar las tierras del circuito a una tierra virtual.
En la parte superior izquierda se tiene el circuito que alimenta al led. En este caso se trata de un led rojo superbrillante.
Finalmente, la parte superior izquierda del circuito es una fotorresistencia en serie con una resistencia normal para formar un divisor de tensión dependiente de la cantidad de luz incidente. Este es el transductor. La señal obtenida se filtra por medio del condensador de 1uF y la resistencia de 68k (En realidad debería de ser de 560k, para obtener una frecuencia de corte de 0.28 Hz). Una vez eliminadas las frecuencias bajas se eliminan las altas frecuencias con el filtro activo que además es un amplificador no inversor. Su frecuencia de corte es de 1.6 Hz aproximadamente, con una amplificación de aproximadamente 212 veces.
El circuito armado se me quedó como sigue (muy feo pero funciona 
)
Algo importante es que el emisor de luz y el detector de la misma deben estar bien firmes y de ser posible eliminar la luz ambiental para minimizar ruidos en nuestro sistema. Yo los coloqué es en una caja de las que manda microchip con sus integrados.
El dedo se coloca en medio y se cierra la caja como si fuera un “sándwich de dedo”
Y lo que obtenemos es una bonita señal como la que se ve en la siguiente foto.
Se puede observar que la señal tiene un offset de aproximadamente 500 mV por lo que debemos aún hacer un poco más de acondicionamiento dependiendo de nuestra aplicación. Sin embargo, para efectos demostrativos esto ya es suficiente.
* Con datos de: http://www.cs.tau.ac.il/~nin/Courses/Workshop12a/PPG%20Sensor%20System.pdf
lunes, 25 de julio de 2011
Redes neuronales
Las redes neuronales artificiales es un método desarrollable en computadoras que sirve para análisis de datos de una forma parecida a como el cerebro animal realiza el procesamiento.
Básicamente se trata de una interconexión de neuronas. Cada una de ellas puede tener múltiples entras y salidas. Las salidas puede variar de acuerdo a las entradas activadas disponibles. Cada neurona puede tratar diferente la activación de una entrada. Por ejemplo, basándonos en la figura de de abajo, la entrada 1 de la capa oculta puede enviar una salida positiva a la capa de salida cuando todas sus entradas son activas mientras que la neurona 2 de la capa oculta puede enviar una salida negativa cuando todas sus entradas son activas.
Dependiendo de la neurona, a cada entrada se le puede asignar un peso diferente haciendo que incremente la salida o que la inhiban completamente.
Esto puede hacer que una red neuronal sea muy compleja, dependiendo del número de entradas, salidas, neuronas y capas.
- Cada neurona puede ser modelada como una simple sumadora de entradas o tan compleja como una serie de ecuaciones diferenciales o cualquier otro modelo que reaccione a las entradas y proporcione una salida.
- La red también se puede hacer de modo que la información fluya en solo una dirección o de modo que fluya en forma cíclica hasta alcanzar la salida.
- Todas las neuronas puede ser actualizadas simultáneamente o con retardos entre las señales.
- Las respuestas de las neuronas a las entradas puede ser determinística o aleatoria.
En fin, las variaciones pueden ser interminables.
Existen modelos de redes neuronales ya probados o teóricamente ejecutables. Algunos son muy lentos, o requieren procesos de entrenamiento que no existen lo que los hace imprácticos para aplicaciones en la vida real.
ENTRENAMIENTO DE UNA RED NEURONAL
Entrenar redes es seleccionar los pesos o procedimientos dentro de cada neurona para obtener una salida deseada con un determinado set de entradas.
Por ejemplo, si una red va a ser empleada para detección de cáncer por medio de imágenes. Su entrenamiento consistirá en un set de imágenes que se sabe provienen de casos de cáncer e imágenes que provienen de sujetos sanos. El entrenamiento consistirá en determinar los pesos de cada entrada y el modelo de la neurona para determinar que imágenes provienen de sujetos sanos y cuales provienen de sujetos enfermos. Por regla general, el set de imágenes de entrenamiento no pueden ser usadas después para evaluar el sistema ya que formaron parte del entrenamiento. Sin embargo, existen ciertas técnicas que permiten usarlas aunque con menor grado de fiabilidad.
Referencias:
1) Timonthy Masters, Practical neural networks recipes in c++, 1993
2) Nicholas Jay Cotton, A neural network implementation on embedded systems. accesed on 26 July 2011. http://etd.auburn.edu/etd/bitstream/handle/10415/2244/Dissertation%20Final.pdf?sequence=4
3) Wikipedia, Red neuronal artificial, http://es.wikipedia.org/wiki/Red_neuronal_artificial
viernes, 5 de noviembre de 2010
Entendiendo la transformada discreta de Fourier
En un procedimiento matemático usado para determinar el contenido armónico o de frecuencia de una señal con miles de aplicaciones en la ingeniería, física, economía, etc.
Pero, veamos en términos mundanos como funciona esto y para que nos puede ser útil.
EJEMPLO TOTALMENTE FICTICIO E IMAGINARIOÑ, valores y señales no son reales. Supongamos que tenemos una máquina que puede medir las ondas eléctricas del cerebro, (Electro encefalograma) y que que esa maquina nos entrega una señal variable en el tiempo como la que se muestra en la figura A. 
Sabemos que en esa señal es la suma de varias ondas eléctricas generadas en el cerebro. También sabemos que el cerebro genera ondas a frecuencias bien definidas para para diferentes estados de ánimo. Por ejemplo, una señal de 2Hz cuando el sujeto está mintiendo y una señal de 5Hz es cuando el sujeto esta diciendo la verdad, etc. Tenemos esta señal que, supongamos pertenece a un terrorista bajo interrogatorio. Queremos saber si esta diciendo la verdad o esta mintiendo respecto a la colocación de la bomba X.
¿Cómo podemos saber si esta mintiendo o diciendo la verdad si sólo tenemos una señal sin aparentes pistas?
Podríamos hacerlo de varias maneras pero se trata de que aquí haga su aparición la famosa Transformada Discreta de Fourier (DFT). :-)
La DFT toma esa señal y nos entrega otra indicando claramente cuales son las frecuencias que conformas la señal original. algo así.
Así es, la DFT no entrega una serie de datos que graficados nos indican que señal sinusoidal tiene más alto contenido de energía y por tanto esa señal es la predomina pero oculta entre otras muchas señales menores. En este caso un pico a 2Hz nos indica que el sujeto está mintiendo. :-)
Bueno, ya que vimos una de las posibles aplicaciones de la DFT llego el momento de ver como se calcula.
El calculo de la DFT se origina con esta “sencilla ecuación”, la transformada de Fourier continua. X(F) es una señal en el dominio de la frecuencia, es decir que varia con la frecuencia como la que vimos arriba indicándonos el pico en 2Hz. x(t) es la señal en el tiempo, como la que vimos arriba entrando a la caja de la DFT y lo demás son “detalles” matemáticos que veremos mas adelante :-)
La formula de arriba esta para una señal continua pero en ahora con el uso de las computadoras, casi siempre tenemos señales discretas, es decir, solo muestras de una señal analógica tomadas a una velocidad llamada frecuencia de muestreo, en otras palabras, cada cierto tiempo se mide el valor de la señal y se guarda ese valor. Si leemos y guardamos el valor de una señal 100 veces cada segundo, tenemos una frecuencia de muestreo de 100Hz, Para analizar ese tipo de señales la formula de arriba se re escribe como;
Y cambiando esa “intimidante” e base del logaritmo natural a su notación trigonométrica tenemos:
Donde;
X(m)=Cada componente m de la salida en función de la frecuencia. X(0),X(1),X(2),X(3),….X(m),
m= Índice de la DTF en el dominio de la frecuencia. m=1,2,3,4…..N-1
x(n)= La secuencia de muestras de entrada de la señal original x(0),x(1),x(2),x(3),x(4),…..x(n)
n= Índice en el dominio del tiempo de las muestras de entrada n=0,1,2,3,4…..N-1
j= numero imaginario (por ahora no le hacemos caso)
N=Numero de muestras de la secuencia de entrada y al mismo tiempo, numero de puntos de frecuencia de la DFT de salida que serán tomados en cuenta.para nuestra DFT.
Supongamos que vamos a calcular la DFT para una señal de N=4, es decir, tomamos sólo 4 muestras de la señal
Sustituyendo valores para m y n=0 y expandiendo la sumatoria tenemos;
Hacemos lo mismo para n y m=1
así hasta m y n=3
Luego, simplemente hacemos las operaciones indicadas y ya tenemos nuestra flamante DFT!!! :-)
Pero que nos indican esos X(0),X(1), X(2), X(3), que obtuvimos después de tanta operación? Bueno, como se habrán podido dar cuenta después de tanta repetición de operaciones, cada X(m) es la suma del producto punto a punto entre la secuencia de entrada y una señal sinusoidal compleja. La frecuencia de cada señal sinusoidal esta dada por.
donde:
fs= es la velocidad de muestreo por ejemplo hace rato mencionamos que tomábamos muestras a 100Hz.
N= Como ya explicamos antes, es el numero de puntos que tomamos para hacer la DFT, entre más grande el valor de N, más alta la resolución.
Por ejemplo, si N=4 y Fs=100 tenemos que la frecuencia de cada sinusoidal aumenta fs/N a termino a termino. en este caso 100/4=25Hz
Así pues,
X(0)= primer termino de frecuencia cuyo valor es 0Hz
X(1)= segundo termino de frecuencia cuyo valor es 25Hz
X(2)= tercer termino de frecuencia cuyo valor es 50Hz
X(3)= cuarto termino de frecuencia cuyo valor es 75Hz
Las graficas mostradas al inicio tenían un valor de N de 1024 puntos por lo que cada termino incrementaba 0.097Hz.
Recordemos que cada Xm es una función sinusoidal con un valor real y un valor imaginario que podemos representar gráficamente como se muestra abajo
En términos más comunes, X0 nos da la magnitud de cualquier componente de 0Hz contenido en la señal, X(1) nos da el termino de cualquier componente de 25Hz y así sucesivamente. Sí comparamos esos Xm podemos saber en que frecuencia el valor es mas grande y por lo tanto que frecuencia domina en la señal de entrada.
Generalmente nos interesa el “poder” de esa señal dominante así que calculando ese punto que representa la señal compleja tenemos:
y
Magnitud y fase de la señal.
La potencia de esa señal y que es lo que frecuentemente se usa y se conoce como espectro de potencias se calcula elevando al cuadrado la magnitud. Así;
De esta “simple” manera podemos calcular el espectro en frecuencia de una señal que nos dirá cual componente de frecuencia es más grande y así inferir que frecuencia está conformando principalmente la señal de entrada.
Fácil, no?
Basado en: Understanding digital signal processing, Richard G. Lyons
