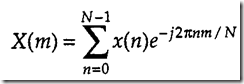viernes, 5 de noviembre de 2010
Entendiendo la transformada discreta de Fourier
En un procedimiento matemático usado para determinar el contenido armónico o de frecuencia de una señal con miles de aplicaciones en la ingeniería, física, economía, etc.
Pero, veamos en términos mundanos como funciona esto y para que nos puede ser útil.
EJEMPLO TOTALMENTE FICTICIO E IMAGINARIOÑ, valores y señales no son reales. Supongamos que tenemos una máquina que puede medir las ondas eléctricas del cerebro, (Electro encefalograma) y que que esa maquina nos entrega una señal variable en el tiempo como la que se muestra en la figura A. 
Sabemos que en esa señal es la suma de varias ondas eléctricas generadas en el cerebro. También sabemos que el cerebro genera ondas a frecuencias bien definidas para para diferentes estados de ánimo. Por ejemplo, una señal de 2Hz cuando el sujeto está mintiendo y una señal de 5Hz es cuando el sujeto esta diciendo la verdad, etc. Tenemos esta señal que, supongamos pertenece a un terrorista bajo interrogatorio. Queremos saber si esta diciendo la verdad o esta mintiendo respecto a la colocación de la bomba X.
¿Cómo podemos saber si esta mintiendo o diciendo la verdad si sólo tenemos una señal sin aparentes pistas?
Podríamos hacerlo de varias maneras pero se trata de que aquí haga su aparición la famosa Transformada Discreta de Fourier (DFT). :-)
La DFT toma esa señal y nos entrega otra indicando claramente cuales son las frecuencias que conformas la señal original. algo así.
Así es, la DFT no entrega una serie de datos que graficados nos indican que señal sinusoidal tiene más alto contenido de energía y por tanto esa señal es la predomina pero oculta entre otras muchas señales menores. En este caso un pico a 2Hz nos indica que el sujeto está mintiendo. :-)
Bueno, ya que vimos una de las posibles aplicaciones de la DFT llego el momento de ver como se calcula.
La formula de arriba esta para una señal continua pero en ahora con el uso de las computadoras, casi siempre tenemos señales discretas, es decir, solo muestras de una señal analógica tomadas a una velocidad llamada frecuencia de muestreo, en otras palabras, cada cierto tiempo se mide el valor de la señal y se guarda ese valor. Si leemos y guardamos el valor de una señal 100 veces cada segundo, tenemos una frecuencia de muestreo de 100Hz, Para analizar ese tipo de señales la formula de arriba se re escribe como;
Y cambiando esa “intimidante” e base del logaritmo natural a su notación trigonométrica tenemos:
Donde;
X(m)=Cada componente m de la salida en función de la frecuencia. X(0),X(1),X(2),X(3),….X(m),
m= Índice de la DTF en el dominio de la frecuencia. m=1,2,3,4…..N-1
x(n)= La secuencia de muestras de entrada de la señal original x(0),x(1),x(2),x(3),x(4),…..x(n)
n= Índice en el dominio del tiempo de las muestras de entrada n=0,1,2,3,4…..N-1
j= numero imaginario (por ahora no le hacemos caso)
N=Numero de muestras de la secuencia de entrada y al mismo tiempo, numero de puntos de frecuencia de la DFT de salida que serán tomados en cuenta.para nuestra DFT.
Supongamos que vamos a calcular la DFT para una señal de N=4, es decir, tomamos sólo 4 muestras de la señal
así hasta m y n=3
Luego, simplemente hacemos las operaciones indicadas y ya tenemos nuestra flamante DFT!!! :-)
Pero que nos indican esos X(0),X(1), X(2), X(3), que obtuvimos después de tanta operación? Bueno, como se habrán podido dar cuenta después de tanta repetición de operaciones, cada X(m) es la suma del producto punto a punto entre la secuencia de entrada y una señal sinusoidal compleja. La frecuencia de cada señal sinusoidal esta dada por.
fs= es la velocidad de muestreo por ejemplo hace rato mencionamos que tomábamos muestras a 100Hz.
N= Como ya explicamos antes, es el numero de puntos que tomamos para hacer la DFT, entre más grande el valor de N, más alta la resolución.
Por ejemplo, si N=4 y Fs=100 tenemos que la frecuencia de cada sinusoidal aumenta fs/N a termino a termino. en este caso 100/4=25Hz
Así pues,
X(0)= primer termino de frecuencia cuyo valor es 0Hz
X(1)= segundo termino de frecuencia cuyo valor es 25Hz
X(2)= tercer termino de frecuencia cuyo valor es 50Hz
X(3)= cuarto termino de frecuencia cuyo valor es 75Hz
Las graficas mostradas al inicio tenían un valor de N de 1024 puntos por lo que cada termino incrementaba 0.097Hz.
Recordemos que cada Xm es una función sinusoidal con un valor real y un valor imaginario que podemos representar gráficamente como se muestra abajo
En términos más comunes, X0 nos da la magnitud de cualquier componente de 0Hz contenido en la señal, X(1) nos da el termino de cualquier componente de 25Hz y así sucesivamente. Sí comparamos esos Xm podemos saber en que frecuencia el valor es mas grande y por lo tanto que frecuencia domina en la señal de entrada.
Generalmente nos interesa el “poder” de esa señal dominante así que calculando ese punto que representa la señal compleja tenemos:
y
Magnitud y fase de la señal.
La potencia de esa señal y que es lo que frecuentemente se usa y se conoce como espectro de potencias se calcula elevando al cuadrado la magnitud. Así;
Fácil, no?
Basado en: Understanding digital signal processing, Richard G. Lyons
